Application of Lingchen Technology Motion Control Card M60+E4O4 Trigger Module in Laptop Flatness Measurement
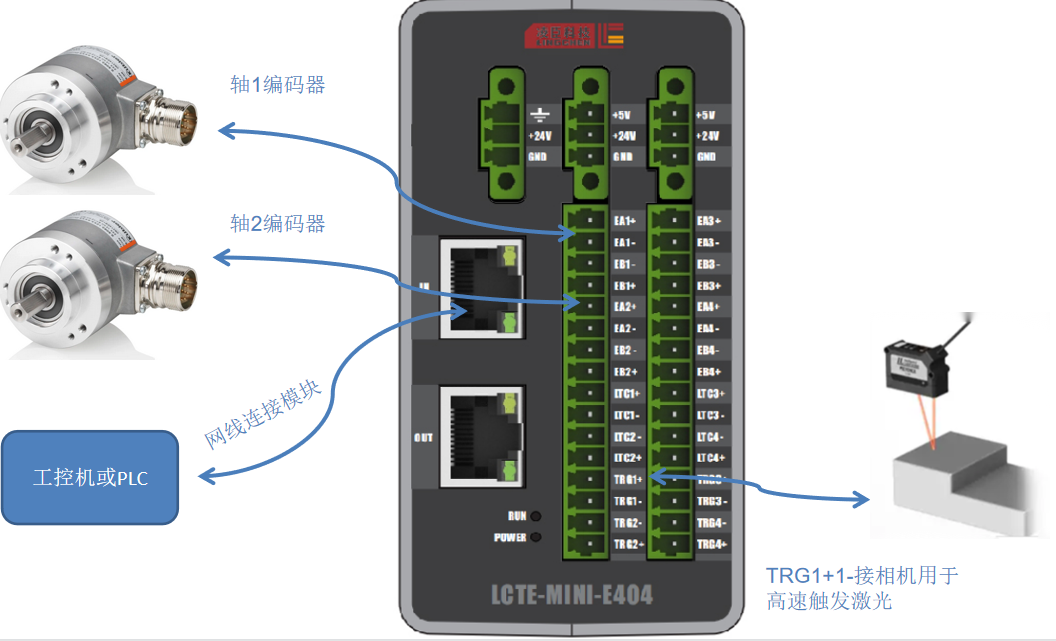
Lingchen Technology E2O2/E4O4, based on feedback from encoders on both axes, sends a trigger signal when the XY axis simultaneously moves to a preset position. It can be used for applications such as flying photography, measuring flatness during movement, and opening and closing glue dispensing valves during movement. It supports up to 4 axis comparison.
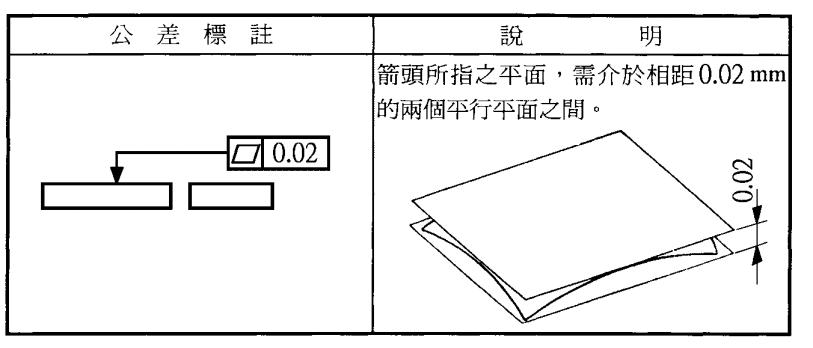
Comparison of flatness measurement methods
M60 continuous trajectory motion
Utilizing the M40's 2-4 axis continuous trajectory motion combined with speed foresight function, achieving non-stop motion and smooth speed curve
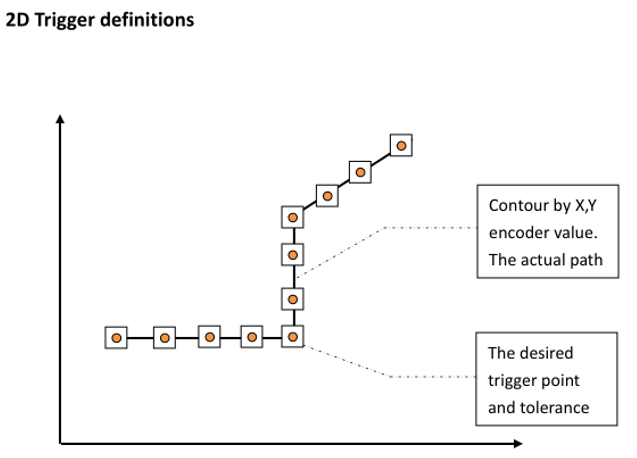
2D Position Comparison Trigger Application
E2O2/E4O4, based on the feedback from the encoders of the two axes, the XY axis simultaneously moves to the preset position and sends a trigger signal. It can be used for applications such as flying photography, measuring flatness during movement, and opening and closing the dispensing valve during movement. It supports a maximum of four axis comparison.
Non-contact point laser altimetry
E4O4 wiring method
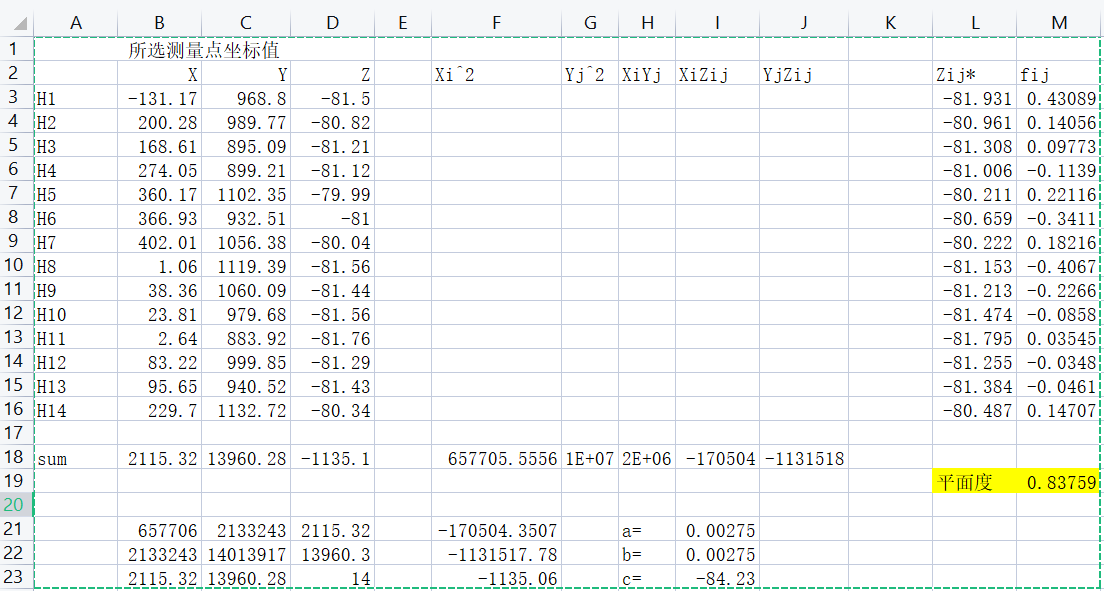
Measurement of flatness of notebook aluminum magnesium alloy
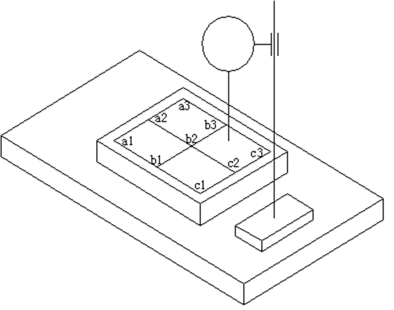
M60 drives the XY axis to trigger laser during flight
Workflow:
1. Pre set the coordinates of the test points required in the following figure to the E4O4 trigger module;
2. M60 drives the XY axis to achieve continuous trajectory motion according to the path shown in the left figure;
3. E4O4 real-time compares coordinates and generates a high-speed trigger signal to the laser upon reaching the preset position. The laser immediately measures the height upon receiving the trigger signal.
4. Substitute the measured height and coordinates into the flatness calculation formula to calculate the product flatness;
Flatness calculation (least squares method)
Using the least squares central plane Sls as the evaluation basis, the difference between the maximum and minimum deviation values of each measurement point relative to the least squares central plane is taken as the flatness error value. The least squares central plane is an ideal plane that minimizes the sum of the squares of the distances from each point on the actual plane to that plane. As shown in the figure, according to the least squares method, the coordinates of each point on the least squares central plane need to be calculated to obtain the flatness error Fls
LINGCHEN TECH
55 Juhua Road, Wangting Town, Xiangcheng District, Suzhou City
Add WeChat
To Obtain a Quote